Yorel
Rêveur
Je ne suis pas un bon pédagogue. 
J'ai très bien saisi, le calcul que je te propose est également une 'chute libre' ; je ne prends pas en compte les résistances des éléments. Ce que je tente de te montrer, c'est que ce cas est plus compliqué qu'il n'y parait, que l'on a une variation de volume, que la hauteur que tu utilises dans ton calcul n'est pas bonne de même que la distance parcourue par l'objet que tu modélises. Dans la mesure ou tu te trompes dans ces valeurs, la comparaison est caduque. Tes équations modélisent le cas d'une balle qu'on aurait laché du haut de la tour. Comparer cela à la chute de la construction n'est pas bon. Tu dois lacher la balle à la bonne hauteur, et lui faire parcourrir la même distance que la construction.
Prenons un cas extrême,
1) Superman arrive, déracine un Building rectangulaire de 50m de haut monte à 600km au dessus de la terre et tient celui-ci dans sa main gauche par le haut, dans sa main droite, il tient une balle de 5cm de diamètre. Et les lâche en même temps dans le vide (on ne considère pas les forces de frottement du à l'air). Comment modélises-tu ce cas ? Tu "réduis" ces 2 objets à deux points (leurs centres de gravité) en lesquels tu vas appliquer ta force de gravité. (tu ne considères que celle-là). Qu'est-ce que tu vas t'apercevoir, c'est que le centre de gravité de ta balle est située une hauteur équivalente à demi-building plus haut que le centre de gravité de ce même building... La comparaison de leur temps de chute n'est pas bonne, ils ne partent pas de la même hauteur.
2) Imaginons tjs le cas précédent, mais concentrons nous sur l'arrivée au sol. Que va être ton temps de chute ? Pour la balle, c'est la différence entre le temps qui correspond à l'arrivée de la balle au sol et l'instant où je l'ai lâché. La distance parcourrue par la balle correspond à la hauteur où je l'ai lâché (à un yota près, le diamètre de la balle étant négligeable). Pour le building de 50m, il en est totalement différent. La distance parcourrue correspond à la hauteur de mon centre de gravité de départ et la hauteur finale de celui-ci. Si mon building reste entier, ne se casse pas au contact du sol (ben oui, on a du super acier, qui ne se casse pas, ne se plie pas, comme dans les rêves les plus fous de Zaene) et que le sol ne s'enfonce pas (on a aussi un super sol), la hauteur finale de ce centre de gravité correspond à la hauteur d'un demi-building. La distance parcourue par les 2 objets est donc différente et la comparaison est une nouvelle fois mise en échec.
Les deux objets vont tomber à la même vitesse, mais l'un parcourt une distance plus petite que l'autre... le temps de chute de celui-ci est donc plus petit également... Pourquoi je parlais d'un temps deux fois plus petit, en réalité. Dans notre cas, ta balle est située au double de la hauteur du centre de gravité du building, tout simplement...
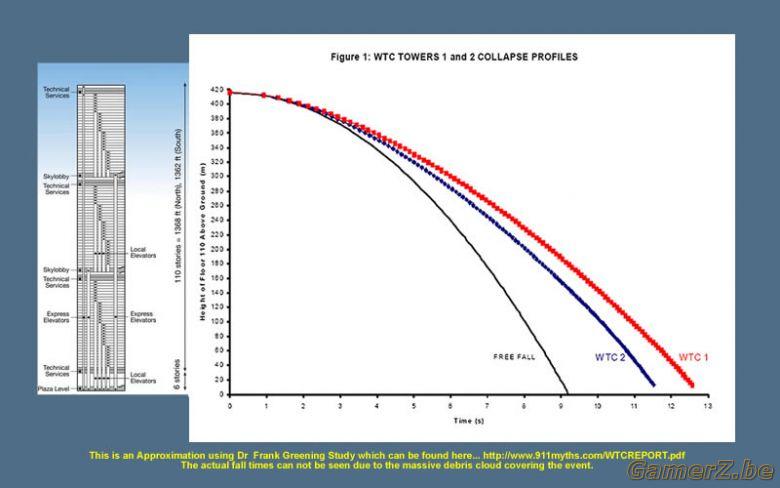
Le temps de chute du building, est de 11 secondes dans la réalité, normalement sans résistance, il aurait du être de 5,5... ( sans compter la variation de volume ).
J'ai très bien saisi, le calcul que je te propose est également une 'chute libre' ; je ne prends pas en compte les résistances des éléments. Ce que je tente de te montrer, c'est que ce cas est plus compliqué qu'il n'y parait, que l'on a une variation de volume, que la hauteur que tu utilises dans ton calcul n'est pas bonne de même que la distance parcourue par l'objet que tu modélises. Dans la mesure ou tu te trompes dans ces valeurs, la comparaison est caduque. Tes équations modélisent le cas d'une balle qu'on aurait laché du haut de la tour. Comparer cela à la chute de la construction n'est pas bon. Tu dois lacher la balle à la bonne hauteur, et lui faire parcourrir la même distance que la construction.
Prenons un cas extrême,
1) Superman arrive, déracine un Building rectangulaire de 50m de haut monte à 600km au dessus de la terre et tient celui-ci dans sa main gauche par le haut, dans sa main droite, il tient une balle de 5cm de diamètre. Et les lâche en même temps dans le vide (on ne considère pas les forces de frottement du à l'air). Comment modélises-tu ce cas ? Tu "réduis" ces 2 objets à deux points (leurs centres de gravité) en lesquels tu vas appliquer ta force de gravité. (tu ne considères que celle-là). Qu'est-ce que tu vas t'apercevoir, c'est que le centre de gravité de ta balle est située une hauteur équivalente à demi-building plus haut que le centre de gravité de ce même building... La comparaison de leur temps de chute n'est pas bonne, ils ne partent pas de la même hauteur.
2) Imaginons tjs le cas précédent, mais concentrons nous sur l'arrivée au sol. Que va être ton temps de chute ? Pour la balle, c'est la différence entre le temps qui correspond à l'arrivée de la balle au sol et l'instant où je l'ai lâché. La distance parcourrue par la balle correspond à la hauteur où je l'ai lâché (à un yota près, le diamètre de la balle étant négligeable). Pour le building de 50m, il en est totalement différent. La distance parcourrue correspond à la hauteur de mon centre de gravité de départ et la hauteur finale de celui-ci. Si mon building reste entier, ne se casse pas au contact du sol (ben oui, on a du super acier, qui ne se casse pas, ne se plie pas, comme dans les rêves les plus fous de Zaene) et que le sol ne s'enfonce pas (on a aussi un super sol), la hauteur finale de ce centre de gravité correspond à la hauteur d'un demi-building. La distance parcourue par les 2 objets est donc différente et la comparaison est une nouvelle fois mise en échec.
Les deux objets vont tomber à la même vitesse, mais l'un parcourt une distance plus petite que l'autre... le temps de chute de celui-ci est donc plus petit également... Pourquoi je parlais d'un temps deux fois plus petit, en réalité. Dans notre cas, ta balle est située au double de la hauteur du centre de gravité du building, tout simplement...
Le temps de chute du building, est de 11 secondes dans la réalité, normalement sans résistance, il aurait du être de 5,5... ( sans compter la variation de volume ).